Войти в REPEAT

Решения

Разработка 1D-модели системы охлаждения ротора турбогенератора

В статье продемонстрированы методика и результаты расчета 1D-модели системы воздушного охлаждения ротора турбогенератора в ПО REPEAT и сравнение результатов расчета с теплогидравлическим расчетом в другом ПО в 3D-постановке.

Разработка 1D-модели системы охлаждения ротора турбогенератора

Турбогенераторы служат источниками энергии на тепловых и атомных электростанциях и на сегодняшний день сохраняют наибольшую долю в генерирующих мощностях во всем мире.

В силу жестких конструктивных требований к габаритам и необходимости обеспечения большой единичной мощности, турбогенераторы являются самыми нагруженными электрическими машинами по критерию удельной мощности, что сопровождается значительным тепловыделением в обмотках и сердечнике.

В то же время в конструкции любой электрической машины применяются электроизоляционные материалы, которые крайне чувствительны к высоким температурам.

Для того чтобы обеспечить сроки службы продолжительностью 40 и более лет, требуемые для турбогенераторов, необходим жесткий контроль за температурами активных частей турбогенераторов. Это достигается применением крайне сложных систем охлаждения с большим количеством каналов небольшого сечения образующими разветвленные гидравлические цепи.
Теплогидравлические расчеты таких систем охлаждения в 3D-постановке крайне требовательны к вычислительным мощностям, альтернативным вариантов в данном случае может выступать 1D-моделирование.

К преимуществам такого подхода по сравнению с 3D-моделированием можно отнести:

ованием можно отнести:  меньшую требовательность к вычислительным ресурсам;
меньшую трудоемкость при моделировании систем, состоящих из большого числа однотипных элементов;
большую гибкость и простоту редактирования.

Что позволяет моделировать значительно более сложные системы по сравнению с 3D-постановкой, а также значительно сокращать время проектирования электрических машин, особенно на этапе эскизного проектирования.

Цели исследования:
1. Разработка имитационной 1D-модели для определения параметров системы охлаждения ротора турбогенератора;
2. Анализ возможности применения 1D-моделей для оценки работы систем охлаждения электрических машин.

Исходные данные

Параметр	Единица измерения	Значение
Ток в каждом проводнике	А	1240
Температура охлаждающего воздуха на входе в подбазовый канал	°C	40
Среднеарифметическая шероховатость стенок аксиальных каналов	мм	0,1
Среднеарифметическая шероховатость стенок радиальных каналов в проводниках	мм	0,5
Объемный расход воздуха через все каналы: для расчетной точки 1	м³/с	0,020
Объемный расход воздуха через все каналы: для расчетной точки 2	м³/с	0,025
Объемный расход воздуха через все каналы: для расчетной точки 3	м³/с	0,030
Объемный расход воздуха через все каналы: для расчетной точки 4	м³/с	0,035
Объемный расход воздуха через все каналы: для расчетной точки 5	м³/с	0,040

Таблица №1. Параметры модели

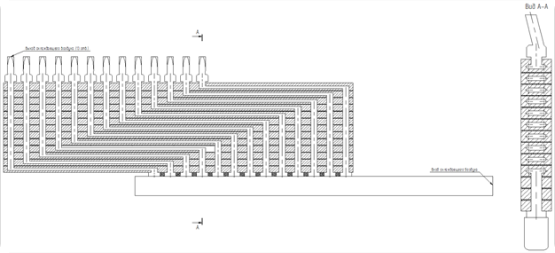
Рис. 1 – Эскиз расчетной области

Рис. 2 – Общий вид расчетной области в другом ПО

Рис. 3 – Результаты расчета в другом ПО

Описание имитационной модели

Для моделирования расчетной области, представленной на Рисунке 1, Рисунке 2 и Рисунке 3, выбрана одномассовая модель с усредненными характеристиками.

Совокупность проводников и изоляции является единой тепловой массой с каналами для интенсивного воздушного охлаждения.

Распределение температур внутри тепловой массы не учитывалось

Схема замещения расчетной области представлена на Рисунке 4.

Тепловыделение в проводниках моделируется блоком «Источник теплового потока», на вход которого поступает значение в соответствии со следующим уравнением, описывающим изменения количества тепла за счет прохождения электрического тока

\( Q = I^2 \cdot R = \frac{I^2 \cdot r_t \cdot L}{S} = \frac{I^2 \cdot \left( r_{20} \cdot \left( 1 + 0.004 \cdot (t - 20) \right) \right) \cdot L}{S}, \)

где \( I \) — сила тока в проводнике, А;

\( R \) — сопротивление проводника, Ом;

\( r_t \) — удельное сопротивление \( (\text{Ом} \cdot \text{мм}^2)/\text{м} \);

\( r_{20} \) — удельное сопротивление при температуре 20 °C, \( (\text{Ом} \cdot \text{мм}^2)/\text{м} \);

\( t \) — температура проводника, °C;

\( L \) — длина проводника, м;

\( S \) — площадь сечения проводника, мм\(^2\).

Температуры в расчетной области были определены посредством моделирования конвективного теплообмена между стенками канала и охлаждающим воздухом, протекающим в них.

Расчет модели выполнен методом косимуляции в программных продуктах САПФИР и REPEAT.

Задача делится на две составляющие: расчет течения воздуха в каналах обмотки ротора и расчет конвективного теплообмена совокупности проводников и воздуха в каналах, каждая из которых решается в соответствующем программном продукте.

САПФИР

САПФИР осуществляет моделирование и расчет течения воздуха с учетом заданной геометрии каналов. В соответствии с исходными данными определяется эпюра давлений.

Потери давления в расчетной области обусловлены потерями на трение, повороты, изменение диаметра и потерями в тройниках.

Потери на поворот [1, с. 287] и изменение диаметра [1, с.126, 165] рассчитываются в соответствии с [1].

Уравнение импульса, используемое в САПФИР для определения расхода газа [3].

\( \frac{l}{s} \cdot \frac{df}{d\tau} - \frac{f^2}{2 \rho s^2} \left( 1 + \xi \right) + kf + \Delta p + \rho g \Delta z = 0 \)

где

\( L \) — длина участка;

\( f \) — массовый расход;

\( \frac{df}{d\tau} \) — производная расхода по времени;

\( s \) — поперечное сечение;

\( \rho \) — плотность;

\( \xi \) — коэффициент гидравлических потерь;

\( k \) — коэффициент, пропорциональный \( \sqrt{p} \), введённый для линеаризации расходной зависимости при \( \Delta p \to 0 \);

\( \Delta p \) — падение давления на участке цепи;

\( g \) — ускорение свободного падения;

\( \Delta z \) — перепад высоты на участке цепи.

\( \xi = \xi_m + \xi_{тр} \)

где \( \xi_m \) — коэффициент местных гидравлических потерь (потери в сужениях/расширениях, поворотах и тройниках), \( \xi_{тр} \) — коэффициент потерь на трение.

Коэффициент гидравлических потерь на трение рассчитывается по формуле:

\( \xi_{тр} = \lambda \frac{L}{d} \)

где

\( \lambda \) — коэффициент трения,

\( d \) — гидравлический диаметр канала.

Коэффициент трения рассчитывается следующим образом [2]:

\( \lambda = \frac{1}{\left(1.8 \log_{10}\left(\frac{6.9}{Re} + \left(\frac{r}{d}\right)^{1.11}\right)\right)^2} \)

где \( Re \) — число Рейнольдса;

\( \frac{r}{d} \) — относительная шероховатость канала.

Моделирование течения воздуха в каналах обмотки ротора выполнено с использованием блоков стандартной библиотеки CMS: «Узел», «Канал», «Граничное условие», «Подпитка», «Внешний источник тепла» (Рисунок 5).

REPEAT

Расчет конвективного теплообмена выполняется в ПО REPEAT.

Параметры воздуха (температура, скорость) передаются из САПФИР в блоки «Конвективная теплопередача с расчетом коэффициента теплоотдачи», где выполняется расчет количества передаваемого тепла. Полученное количество теплоты, отводимое воздухом с поверхности проводников, передается в САПФИР, замыкая, таким образом, расчет уравнений теплообмена.

Для расчета необходимо заполнить соответствующие свойства блока: «Площадь поверхности», «Тип конвекции», «Тип обтекания», «Характерный размер», «Длина трубы», «Смоченный периметр» и «Площадь сечения потока».

Имитационная модель, выполненная в REPEAT представлена на Рисунке 6.

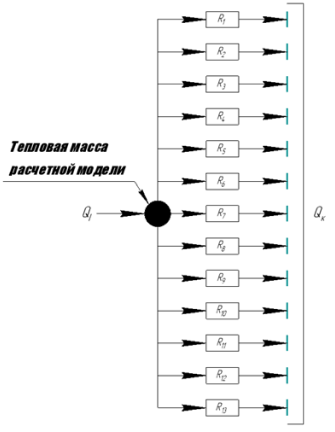
Рис. 4 – Схема замещения

где
\( Q_1 \) — количество теплоты, выделяемой в проводниках при прохождении тока;
\( Q_k \) — количество теплоты, снимаемой с совокупности проводников за счет охлаждения воздухом (13 каналов);

Рис. 5 – Теплогидравлическая модель охлаждающих каналов в САПФИР

Рис. 6 – Модель конвективного теплообмена в ПО REPEAT

1 – Расчет тепловых потоков от охлаждающих каналов; 2 – Расчет теплового потока от протекания тока; 3 – Тепловая масса проводников

Результаты моделирования

Результаты расчета параметров (средняя температура проводников, суммарный тепловой поток, перепад давления в каналах, температура воздуха на выходе из каналов, параметры аксиальных и радиальных каналов) и отклонения от проверочных данных представлены в таблицах 2 – 8. В качестве проверочных данных использованы результаты CFD-расчета в другом ПО.

Таб. 2 – Средняя температура проводников

Таб. 3 – Суммарный тепловой поток

Таб. 2 – Средняя температура проводников