Войти в REPEAT

Решения

Моделирование работы автомобиля с двигателем внутреннего сгорания (ДВС) на платформе REPEAT

Результаты моделирования автомобиля с ДВС, получены на платформе REPEAT. Проведено сравнение с результатами, полученными с помощью другого ПО, аналогичной по параметрам модели.

Блок «ДВС» представляет собой настраиваемый двигатель внутреннего сгорания, который подходит для моделирования двигателей с принудительным зажиганием (spark-ignition) и с самовоспламенением (diesel). Управление блоком доступно либо крутящим моментом, либо физическим сигналом дроссельной заслонки. Блок включает в себя дополнительные динамические параметры такие как инерция коленчатого вала и задержку времени отклика. Также данный блок имеет регулятор скорости, предотвращающий заглох двигателя и улучшающий переходные характеристики.

Блок производит вычисления по следующим уравнениям:

Удельная частота вращения двигателя:

\[ \omega_{N}(\omega) = \frac{\omega}{\omega_{PP}}, \]

где \( \omega \) — текущая скорость;

\( \bar{\omega} \) — скорость при максимальной мощности.

Мощность двигателя представлена третьим полиномом:

\[ P(\omega(\omega_N)) = P_p \cdot p_N(\omega_N); \] \[ p_N(\omega_N) = s_1 \cdot \omega_N + s_2 \cdot \omega_N^2 + s_3 \cdot \omega_N^3, \]

где \( s_i \) — коэффициенты полинома;

\( P_p \) — максимальная мощность.

Блок вычисляет крутящий момент двигателя при полностью открытой дроссельной заслонке, используя полиномиальные коэффициенты согласно:

\[ M(\omega(\omega_N)) = p_1 + p_2 \omega_N + p_3 \omega_N^2; \] \[ p_1 = \frac{s_1 P_p}{\omega_{PP}}; \quad p_2 = \frac{s_2 P_p}{\omega_{PP}}; \quad p_3 = \frac{s_3 P_p}{\omega_{PP}} \]

Блок устанавливает удельную частоту вращения двигателя при максимальной мощности согласно:

\[ \omega_{NPP} = \omega_N(\omega_{NPP}) = 1. \]

Подставляя данного равенства в формулу для \(p_N\) дает

\[ s_1 + s_2 + s_3 = 1 \]

Данное условие нормирует мощность в соответствии с частотой вращения двигателя на максимальной мощности. Блок приравнивает наклон \( p_N(\omega_{PP}) \) нулю, таким образом, что

\[ s_1 + 2s_2 + 3s_3 = 0. \]

Блок определяет удельную частоту вращения двигателя при максимальном крутящем моменте как

\[ \omega_{NPT} = \omega_N(\omega_{PT}) = \frac{\omega_{PT}}{\omega_{PP}} < 1. \]

Где скорость максимальной мощности больше скорости максимального крутящего момента. Блок использует полиномиальную интерпретацию, чтобы найти безразмерный удельный крутящий момент \( m_N \) и установить наклон равным нулю таким образом, что

\[ \frac{dm_N(\omega_{NPT})}{d\omega} = s_2 + 2s_3 \omega_{NPT} = 0. \]

Данное выражение позволяет найти \(s_i\)

\[ s_1 = \frac{3 - 4\omega_{NPT}}{2(1 - \omega_{NPT})}; \quad s_2 = -\frac{\omega_{NPT}}{2(1 - \omega_{NPT})}; \quad s_3 = -\frac{1}{2(\omega_{NPT} - 1)} \]

Вычисление момента ДВС производится по формуле:

\[ M(\omega(\omega_N)) = \frac{2M_P}{3 - \omega_{NPT}}(s_1 + s_2 \omega_N + s_3 \omega_N^2), \]

где \(M_P\) — максимальная мощность.

Замена \(\omega_{NPT}\) приводит уравнение момент \(M(\omega(\omega_N))\) в вид:

\( 2M_p \omega_{PP}^2 - 3P_p \omega_{PP} + P_p \omega_{PT} = 0 \)

Блок ДВС, используя переменные \( M_p \), \( P_p \) и \( \omega_{PT} \), вычисляет максимальные обороты \( \omega_{PP} \) по формуле

\( \omega_{PP} = \frac{3P_p + \sqrt{P_p(9P_p - 8M_p \omega_{PT})}}{4M_p} > \omega_{PT} \).

Блок вычисляет полиномы согласно коэффициентам типа двигателя. При включении тумблера "Дизельный двигатель", блок определяет \( s_i \) согласно значениям приведенной ниже таблицы:

Коэффициент мощности	Тип двигателя
Коэффициент мощности	Принудительное зажигание	Самовоспламенение (дизель)
\( p_1 \)	1	0,6256
\( p_2 \)	1	1,6948
\( p_3 \)	1	-1.3474

Таблица №1. Коэффициенты мощности по типу двигателя

Данная модель состоит из следующих основных элементов:

ДВС;
Шасси с трансмиссией;
Динамика 4-х колесного автомобиля;
Коробка передач (рисунок 2).

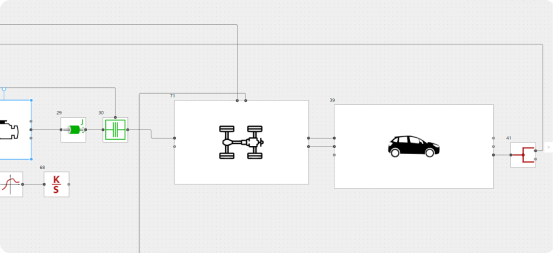
Рис. 1 – Схема подключения блока “ДВС”

Рис. 2 – Схема коробки передач

Динамика продольного движения описывается с помощью блоков “ Динамика 4-х колесного автомобиля” и “Шасси с трансмиссией”. Расчет скорости движения автомобиля производится через его ускорение, определяемое из уравнения второго закона Ньютона для нахождения результирующей силы, приводящей автомобиль в движение. Уравнение имеет следующий вид:

\[ m \cdot a = F_T + F_R + F_D + F_W. \]

В данной формуле \( m \) — масса автомобиля в кг, \( a \) — ускорение, сообщаемое автомобилю в м/с²,

\( F_T \) — сила сухого трения между шинами и поверхностью дороги, равная:

\[ F_T = F_{T, f} + F_{T, r}, \]

где \( F_{T,f} \) — сила трения между передними шинами и дорогой, равная:

\( F_{T,f} = \frac{\eta \cdot N_{fd} \cdot N_m}{r_t} \cdot T + B \cdot U_b \)

где \( \eta \) — КПД в о.е.;

\( N_{fd} \) — передаточное число главной передачи;

\( N_m \) — число электродвигателей;

\( r_t \) — радиус колеса в м;

\( B \) — коэффициент усиления торможения;

\( U_b \) — относительное положение педали торможения;

\( F_{T,r} \) — сила трения между задними шинами и дорогой, равная:

\( F_{T,r} = B \cdot U_b \).

\( F_{T,f} \) — сила трения между задними шинами и дорогой, равная:
\( F_{T,r} = B \cdot U_b \)

\( F_{R} \) — сила сопротивления движению шин, равна:

\( F_{R,i} = C_R \cdot F_{N,i} \).

\( C_R \) — коэффициент качения, \( F_{N,f} \) — сила, действующая либо на переднюю, либо на заднюю ось трансмиссии и равна:

\( L_{101} \cdot F_{N,f} = m \cdot g \cdot \cos \theta \cdot CG_{r} - m \cdot a \cdot CG_{h} - m \cdot g \cdot \sin \theta \cdot CG_{h} \)
\( L_{101} \cdot F_{N,r} = m \cdot g \cdot \cos \theta \cdot CG_{f} + m \cdot a \cdot CG_{h} + m \cdot g \cdot \sin \theta \cdot CG_{h} \)

где \( L_{101} \) — длина колесной базы в м;

\( F_{N,f}, F_{N,r} \) — силы, действующие на переднюю и заднюю оси трансмиссии автомобиля соответственно (в Н);

\( CG_{h} \) — высота центра масс в м;

\( CG_{f}, CG_{r} \) — расстояние от задней и передней оси до центра масс в м;

\( F_D \) — сила аэродинамического сопротивления, равная:

\( F_D = \frac{1}{2} \cdot \rho \cdot A \cdot C_D \cdot V^2 \)

где \( \rho \) — плотность воздуха в кг/м ³;

\( A \) — фронтальная площадь автомобиля в м²;

\( C_D \) — коэффициент аэродинамического сопротивления;

\( V \) — продольная скорость автомобиля в м/с

\( F_W \) — сила тяжести, равная:
\( F_W = m \cdot g \cdot \sin \theta \),

\( g \) — ускорение свободного падения в м/c ², \( \theta \) — угол наклона дороги в градусах