Solutions

Operation modeling of a car with an internal combustion engine (ICE) on REPEAT platform

Simulation results of a car with ICE, obtained on REPEAT platform. The results obtained with other software similar in parameters to the model were compared with the results obtained with other software.

The ICE is a customizable internal combustion engine that is suitable to simulate spark-ignition and diesel engines. The block control is available either by torque or physical throttle valve signal. The block includes additional dynamic parameters such as crankshaft inertia and response time delay. Also, this block has a speed controller that prevents engine stall and improves transient characteristics.

The block calculates the following equations:

The specific rotation frequency of the engine:

\[ \omega_{N}(\omega) = \frac{\omega}{\omega_{PP}}, \]

where \( \omega \) — current speed;

\( \bar{\omega} \) — speed at maximum power.

Engine power is represented by a third polynomial:

\[ P(\omega(\omega_N)) = P_p \cdot p_N(\omega_N); \] \[ p_N(\omega_N) = s_1 \cdot \omega_N + s_2 \cdot \omega_N^2 + s_3 \cdot \omega_N^3, \]

where \( s_i \) — polynomial coefficients;

\( P_p \) — maximum power.

The block calculates the engine torque at fully open throttle valve using polynomial coefficients according to:

\[ M(\omega(\omega_N)) = p_1 + p_2 \omega_N + p_3 \omega_N^2; \] \[ p_1 = \frac{s_1 P_p}{\omega_{PP}}; \quad p_2 = \frac{s_2 P_p}{\omega_{PP}}; \quad p_3 = \frac{s_3 P_p}{\omega_{PP}} \]

The block sets the specific rotation frequency of the engine at maximum power according to:

\[ \omega_{NPP} = \omega_N(\omega_{NPP}) = 1. \]

Substituting this equality into the formula for \(p_N\) gives

\[ s_1 + s_2 + s_3 = 1 \]

This condition normalizes the power in accordance with the engine rotation frequency at maximum power. Block equates slope \( p_N(\omega_{PP}) \) zero, such that

\[ s_1 + 2s_2 + 3s_3 = 0. \]

The block determines the specific engine rotation frequency at maximum torque as

\[ \omega_{NPT} = \omega_N(\omega_{PT}) = \frac{\omega_{PT}}{\omega_{PP}} < 1. \]

Where the speed of the maximum power is greater than the speed of the maximum torque. Block uses polynomial interpretation to find dimensionless specific torque m_N and set the slope to zero such that

\[ \frac{dm_N(\omega_{NPT})}{d\omega} = s_2 + 2s_3 \omega_{NPT} = 0. \]

This expression allows to find \(s_i\)

\[ s_1 = \frac{3 - 4\omega_{NPT}}{2(1 - \omega_{NPT})}; \quad s_2 = -\frac{\omega_{NPT}}{2(1 - \omega_{NPT})}; \quad s_3 = -\frac{1}{2(\omega_{NPT} - 1)} \]

ICE torque is calculated by the formula:

\[ M(\omega(\omega_N)) = \frac{2M_P}{3 - \omega_{NPT}}(s_1 + s_2 \omega_N + s_3 \omega_N^2), \]

where \(M_P\) — is maximum power.

The replacement \(\omega_{NPT}\) brings the torque equation \(M(\omega(\omega_N))\) to the form:

\( 2M_p \omega_{PP}^2 - 3P_p \omega_{PP} + P_p \omega_{PT} = 0 \)

ICE block using variables \( M_p \), \( P_p \) and \( \omega_{PT} \), calculates the maximum rotations \( \omega_{PP} \) by formula

\( \omega_{PP} = \frac{3P_p + \sqrt{P_p(9P_p - 8M_p \omega_{PT})}}{4M_p} > \omega_{PT} \).

The block calculates polynomials according to the coefficients of the engine type. When "Diesel engine" toggle switch is set to ON, the block determines \( s_i \) according to the table below:

Power factor	Engine type
Power factor	Forced ignition	Self-ignition (diesel)
\( p_1 \)	1	0,6256
\( p_2 \)	1	1,6948
\( p_3 \)	1	-1.3474

Table 1. Power factors by engine type

This model consists of the following main components:

ICE;
Chassis with transmission;
Dynamics of 4-wheel vehicle;
Gearbox unit (Figure 2).

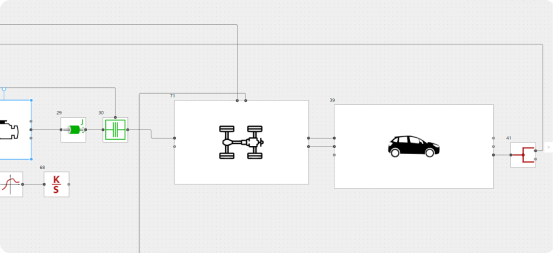
Fig. 1 - Diagram of ICE block connection

Fig. 2 - Diagram of gearbox unit

The dynamics of longitudinal movement is described using blocks "Dynamics of a 4-wheel vehicle" and "Chassis with a transmission." The speed of the vehicle is calculated using its acceleration, which is determined from Newton's second law equation to find the resultant force driving the vehicle. The equation is as follows:

\[ m \cdot a = F_T + F_R + F_D + F_W. \]

In this formula \( m \) — vehicle weight in kg, \( a \) — acceleration given to the vehicle in m/s²,

\( F_T \) — dry friction force between tires and road surface equal to:

\[ F_T = F_{T, f} + F_{T, r}, \]

where \( F_{T,f} \) — friction force between front tires and road, equal to:

\( F_{T,f} = \frac{\eta \cdot N_{fd} \cdot N_m}{r_t} \cdot T + B \cdot U_b \)

where \( \eta \) — efficiency in s.u.;

\( N_{fd} \) — final drive ratio;

\( N_m \) — - number of electric motors;

\( r_t \) — wheel radius in m;

\( B \) — braking gain ratio;

\( U_b \) — relative position of braking pedal;

\( F_{T,r} \) — friction force between rear tires and road, equal to:

\( F_{T,r} = B \cdot U_b \).

\( F_{T,f} \) — friction force between rear tires and road, equal to:
\( F_{T,r} = B \cdot U_b \)

\( F_{R} \) —tire movement resistance force equal to:

\( F_{R,i} = C_R \cdot F_{N,i} \).

\( C_R \) — rolling coefficient, \( F_{N,f} \) — force acting either on the front or rear axle of the transmission and equal to:

\( L_{101} \cdot F_{N,f} = m \cdot g \cdot \cos \theta \cdot CG_{r} - m \cdot a \cdot CG_{h} - m \cdot g \cdot \sin \theta \cdot CG_{h} \)
\( L_{101} \cdot F_{N,r} = m \cdot g \cdot \cos \theta \cdot CG_{f} + m \cdot a \cdot CG_{h} + m \cdot g \cdot \sin \theta \cdot CG_{h} \)

where \( L_{101} \) — wheelbase length in m;

\( F_{N,f}, F_{N,r} \) — forces acting on the front and rear axles of the vehicle transmission, respectively (in N);

\( CG_{h} \) — height of the center of mass in m;

\( CG_{f}, CG_{r} \) — distance from the rear and front axle to the center of mass in m;

\( F_D \) — aerodynamic resistance force equal to:

\( F_D = \frac{1}{2} \cdot \rho \cdot A \cdot C_D \cdot V^2 \)

where \( \rho \) — air density in kg/m ³;

\( A \) — front area of the electric vehicle in m²;

\( C_D \) — aerodynamic resistance coefficient;

\( V \) — longitudinal speed of the vehicle in m/s

\( F_W \) — gravity force equal to:
\( F_W = m \cdot g \cdot \sin \theta \),

\( g \) — acceleration of gravity in m/s ², \( \theta \) — the slope of the road in degrees